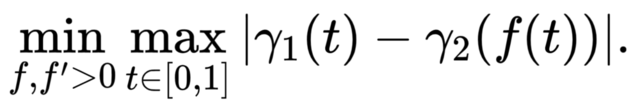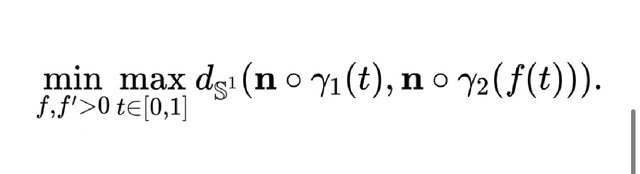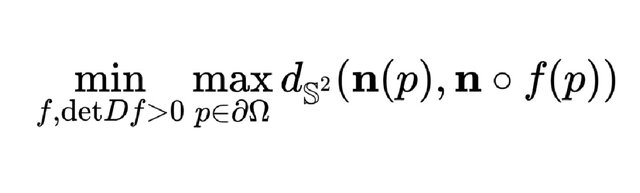StillWandering 写了: ↑26 2月 2024, 08:13“遛狗”定理
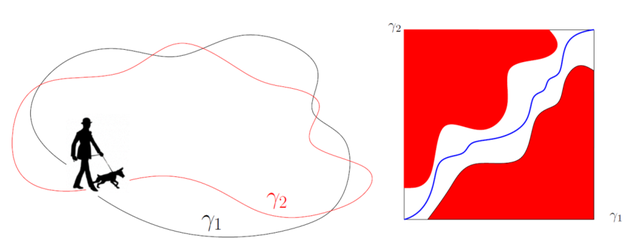
如图3左帧所示,假设有一位朋友遛狗,这位朋友在平面上的轨迹是一条封闭曲线1(t),狗的轨迹是另外一条封闭曲线1(s),人和狗都是逆时针行走,在任意时刻,在各自轨道上一直面向前方,从不回头(但是走过一圈,整体上绕回到起点)。
图3. 在各种遛狗方式中,最短的牵狗绳长度等于曲线间的Frechet距离。Frechet距离:同一时刻人和狗的位置之间有个对应关系,这自然给出了轨道间的一个同胚映射⨍:1→2,等价的我们用参数来表示s=⨍(t)。由人和狗都不回头的假定,我们自然有⨍'(t)>0对于任意时刻t都成立。那么不同的遛狗方式对应着不同的同胚映射⨍。如果固定一个遛狗方式⨍,牵狗绳的长度不小于人和狗之间任意时刻的最大距离maxt|1(t)-2(⨍(t))。在所有可能的遛狗方式中,最短的牵狗绳长度等于:
我们将可能的最短牵狗绳长度定义为1和2的Frechet距离。
在计算几何中,人们对于Frechet距离的算法已经有了充分的研究。如图3右帧所示,我们用横轴表示的参数1(t),纵轴表示的参数2(s)。任何同胚映射⨍:1→2,满足⨍(0)=0可以表示成一条连接对角点的曲线,曲线在水平和铅直两个方向都是单调的。给定一个ℇ>0,对于正方形内任意一点(t,s),如果1(t)-2(s)>=ℇ,我们将其绘为红色,反之为白色。那么白色区域为自由区域,红色区域为禁止区域。如果白色区域中存在一条水平、铅直都单调的曲线,连接对角点,则这两条曲线的Frechet距离小于ℇ。实际计算中,我们可以用二分法来搜索ℇ,找到1,2的Frechet距离。
法向Frechet距离:类似的,假如1和2的正则性较好,例如它们是C1光滑的,则沿着曲线法向量是良定义的。由此我们可以定义法向Frechet距离:我们将人和狗所在位置之间的距离换成人和狗所在点处的外法向量之间的距离,写成公式就是:
这里dS1(.,.)是单位圆上的测地距离。
倾斜条件:给定平面区域间的最优传输映射,边界曲线∂Ω和∂∑是二阶光滑的,⨍,g满足一定的光滑性条件,那么最优传输映射可以拓展到边界上,T:Ω→∑,并且满足所谓的倾斜性条件(Obliqueness Condition),即给定边界上一点p∈∂Ω,(n(p),noT(p))>=0,即边界点的法向量和对应像点的法向量夹角小于等于直角。
遛狗定理:假设已知定义在平面区域上概率分布,(µ,Ω)和(v,∑),这里概率密度函数满足比较宽泛的正则性条件,边界曲线∂Ω和∂∑是二阶光滑;如果∂Ω和∂∑的法向Frechet距离大于π/2,则最优传输映射非连续,存在奇异集合。假如最优传输映射T:Ω→∑不存在奇异集合,Brenier势能函数全局可微,那么T可以拓展到边界上,并且在边界上的限制是同胚T∂µ:∂Ω→∂∑,并且满足倾斜条件,因此∂Ω和∂∑的法向Frechet距离不大于直角,矛盾。于是我们得出结论:存在奇异集合,最优传输映射在奇异集合上间断。
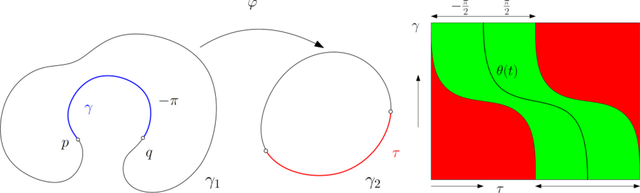
曲率条件:由遛狗定理,我们可以给出一些最优传输映射存在奇异点的曲率条件。如图4左帧所示,如果有一段曲线∂µ,总曲率小于⊂∂µ,即存在:∫rk(t)dt<-π。
∑为凸集,那么最优传输映射必定存在奇异集合。如图4右帧所示,横轴为∂∑,纵轴为⊂∂µ。两条曲线都采用弧长参数。对于任意一点(t,s),如果∂Ω(t)处的法向量∂∑(s)与处的法向量夹角大于π/2,我们将其绘为红色,否则为绿色。则绿色区域为自由区域。的起点为p,的终点为q,右侧长方形底边对应p,顶边对应q。底边和顶边的绿色区域恰好互补,那么绿色区域中不存在沿着水平方向和铅直方向都单调的曲线。这意味着∂Ω和∂∑的法向Frechet距离一定大于π/2,必然存在奇异集合,最优传输映射在奇异集合上非连续。这种情形下,最优传输映射无法用深度神经网络直接表示。
推广和展望
高维的最优传输映射比平面上的最优传输映射复杂,但是同样的想法可以推广。例如在三维情形,假设Ω,∑⊂R3是三维空间中的区域,其边界∂Ω和∂∑是C2光滑曲面,其法向Frechet距离定义为:
如果法向Frechet距离大于π/2,则最优传输映射存在奇异集合。遛狗定理给出了奇异集合存在的充分条件,必要条件目前尚未清楚。奇异集合的拓扑刻画依然存在很多开放的问题。这些基本问题需要基础数学家给出解答。
在深度学习中,隐空间中的数据分布支集往往具有复杂拓扑,几何上也不具备凸性,传输映射不可避免地存在奇异集合,因此深度神经网络无法表达这种非连续的映射。为了避免模式坍塌,我们可以用神经网络表达Brenier势能函数,或者采用特定的数值逼近方法。另一方面,Monge-Ampere方程强烈非线性,高维最优传输映射计算复杂度很高。如何设计更加高效的算法,和更加适合求解的硬件,这也为计算机科学家提出了挑战。
我们相信未来最优传输映射的正则性理论会进一步发展,能够给出奇异集合的深刻洞察和刻画,从而更好地指导深度学习的统计理论;也相信深度学习领域会有更多基于最优传输理论的模型被提出并深入探索,从根本上克服模式坍塌等瓶颈问题,并且使得黑箱变得透明。
下一次遛狗的时候,希望朋友们能够深入思考一下深度学习的模式坍塌问题,也思考一下如何在整个地球表面“遛鹰”,从而体会高维的Frechet距离。
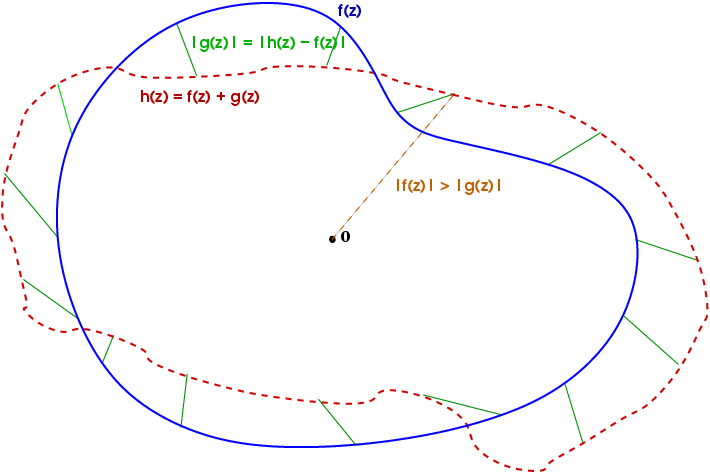
巧了,单复变函数 中用来比较两个全纯函数在单连通域上的零点的 Rouche Theorem 也经常用遛狗来解释。
https://en.wikipedia.org/wiki/Rouch%C3%A9%27s_theorem